Sans titre

4 - Comment communiquer avec Marc ?

4-1 Avec la voix ( le son )

4-1-1 Comment le son se propage-til dans l'air ? Aidez vous de l'animation ci dessous pour expliquer. Les points représentent les particules (molécules) d'air.

4-1-2 Est ce que le son peut arriver sur Mars ?

4-1-3 A quelle vitesse se propage le son dans l'air ?

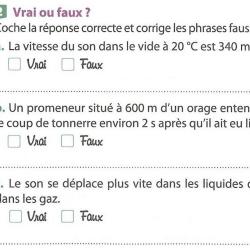
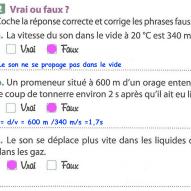
Entrainement :

4-1-4 La vitesse du son est de 340 m/s, cela signifie que le son parcourt 340 m à chaque seconde.

a ) Quelle distance parcourt le son en 30 secondes ?

b) Quelle distance parcourt-t-il en 3 min ? (aide convertir le minutes en secondes)

c ) Combien de temps lui faut-il pour parcourir 680 m ?

d ) Combien de temps lui faut-il pour parcourir 3400 m ?

e) Combien de temps lui faut-il pour parcourir 1km ? (aide convertir 1km en m)

f ) Combien de temps faudrait-il pour qu'un signal sonore quitte l'atmosphère (800km) ? (résultat en min)

Aide :

il faut convertir 800km en m.

1 km = 1000 m

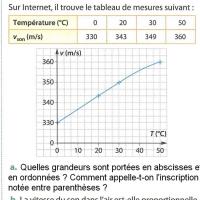
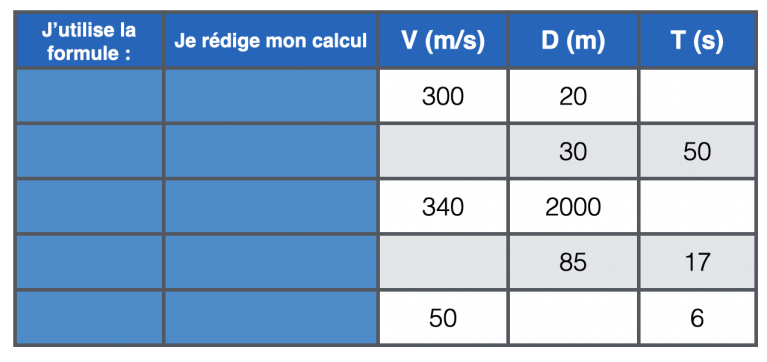
Complete le tableau suivant :

4-1-5-a Expliquez le phénomène dans la scéne ci-dessous :

4-1-5-b Déterminez à quelle distance se trouve l'embarcation du volcan ?

(vous pouvez vous aider du graphique ci-dessous )

4-1-6 Une falaise renvoye l'écho.

Une personne lançant un appel l’entend revenir 4 secondes après.

A quelle distance de la falaise est-elle ? La vitesse du son est 340 m/s

aide :

4-2 Communiquer en Morse :

4-2-1 Réalisez un circuit électriqe pour communiquer à l'aide d'un signal lumineux.

Etablir la liste du matériel. (faire le dessin)

5- A la vitesse de la lumière :

5 - 1 A quelle vitesse se déplace la lumière ?

5 - 2 Entre une onde "téléphonique" et la lumineuse qui va le plus vite ?

Entrainement

5-3 L'orage est à 10 km.

5-3-1 Combien de temps faut-il au tonnerre pour arriver ?

5-3-2 Combien de temps faut-il à l'éclair pour arriver ?

6- le son dans l'eau :

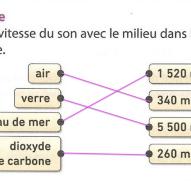
6 -1 A quelle vitesse se déplace le son dans l'eau ?

6 - 2 A quelle vitesse se déplace le son dans le verre ?

6 - 3 Pour quelle raison ce son se déplace-t-il plus vite dans ces deux matériaux ?

Partie de pêche :

Utiliser un tableau de proportionnalité :

6 - 4 Calculez la durée entre l’émission et la réception du signal sonore dans la position A

6 - 5 Calculez le profondeur du fond marin à la position B

Série 1 ex

Série 2 ex

Attention les ex 7 et 10 sont en bonus pour la 4e

Ex 5 :

5-a. Pourquoi y a-t-il un décalage de temps entre l'observation de l'éclair et le son entendu ?

Le décalage de temps s'explique par la différence de vitesse entre la lumière (l'éclair) et le son (le tonnerre).

La lumière voyage extrêmement vite (à environ 300,000 km/s).

Le son voyage beaucoup plus lentement (à environ 340 m/s, soit 0.340 km/s).

A RETENIR

Comme la lumière arrive instantanément à nos yeux, mais le son met un certain temps pour parcourir la même distance, on voit l'éclair avant d'entendre le coup de tonnerre.

5-b. À quelle distance environ d'Anna a lieu l'orage ?

1. Données :

Temps mesuré (t) : 5 secondes

Vitesse du son dans l'air (v) : 340 m/s

2. Relation :

La distance (d) parcourue est égale à la vitesse (v) multipliée par le temps (t).

d=v×t

3. Calcul :

d=340 m/s×5 s

d=1,700 m

4. Réponse :

La distance entre Anna et l'orage est d'environ 1,700 m/s

5-c. Trouve une méthode simple pour déterminer rapidement la distance approximative te séparant d'un orage.

3 s×340 m/s≈1,020 m

A RETENIR

on peut dire que le son a fait 1 km toutes les 3s (2 km en 6s)

6-a. Estime approximativement à quelle distance se trouve le train.

Données :

Temps de décalage (t) entre les deux observations : 15 secondes

Vitesse du son dans l'air Vair) : environ 340 m/s (ou 0.340 km/s)

A SAVOIR : Le son voyage beaucoup plus vite dans l'acier que dans l'air.

Averell entend le son instantanément (le temps de parcours dans l'acier est très court).

Lucky Luke (dans l'air) entend le son 15 secondes plus tard.

Ces 15 secondes correspondent au temps mis par le son pour parcourir la distance dans l'air.

Calcul de la distance (d) :

d= Vair x t

d= 340 m/s ×15 s

d= 5 100 m

Réponse :

Le train se trouve approximativement à 5,100 m (soit 5.1 km) des Dalton.

6-b. Combien de temps a mis le bruit du train pour parvenir jusqu'à Averell ?

Données :

Distance (d) : 5,100 m (ou 5.1 km)

Vitesse du son dans l'acier (Vacier) : 5 km/s (soit 5,000 m/s)

Calcul du temps (t) :

t= Vacier x d

t= 5 km/s x 5.1 km =1.02 secondes

Réponse : Le bruit a mis seulement 1.02 secondes pour parvenir jusqu'à Averell.

6-c. Averell a-t-il utilisé une méthode efficace pour détecter l'arrivée du train ?

Réponse : Oui, la méthode d'Averell est très efficace.

A RETENIR

Le son voyage beaucoup plus vite dans un solide (comme l'acier du rail) que dans un gaz (l'air).

En collant son oreille sur le rail, il entend le sifflement du train presque 14 secondes plus tôt que Lucky Luke.

EXERCICE BONUS (pour la 4e)

7-a. Quelles grandeurs sont portées en abscisses et en ordonnées ?

Comment appelle-t-on l'inscription notée entre parenthèses ?

SAVOIR :

Abscisses (axe horizontal) : La Température (T) en degrés Celsius (°C).

Ordonnées (axe vertical) : La Vitesse du son (v) en mètres par seconde (m/s).

L'inscription notée entre parenthèses, comme (°C) ou (m/s), s'appelle l'unité de mesure.

7-b. BONUS : La vitesse du son dans l'air est-elle proportionnelle à la température ?

Réponse : Non, la vitesse du son n'est pas proportionnelle à la température.

Un graphique représentant une situation proportionnelle devrait être une droite qui passe par l'origine du repère (le point (0;0)).

Ici, la droite ne passe pas par l'origine. Par exemple, à 0 °C, la vitesse n'est pas 0 m/s, mais 330 m/s.

7-c. Le jardin mesure 600 m de long. Entre un air à 0 °C et un air à 30 °C, la différence de durée du trajet du son sur la longueur du jardin serait-elle perceptible ?

1. Déterminer les vitesses dans le tableau :

À 0 °C : v1 = 330 m/s

À 30 °C : v2 = 349 m/s

La distance (d) est 600 m.

2. Calculer les temps de trajet (t = d / v) :

Temps à 0 °C (t 1 ) : t1 = 330 m/s x 600 m ≈1.818 s

Temps à 30 °C (t 2) : t2 = 349 m/s x 600 m ≈1.719 s

3. Calculer la différence de durée :

t1−t2 ≈1.818 s−1.719 s ≈ 0.099 seconde

4. Conclure :

La différence de durée est d'environ 0.1 seconde.

Non, cette différence de durée ne serait pas perceptible par l'oreille humaine, qui ne peut pas distinguer des décalages aussi courts sans appareil de mesure précis.

8-a. Quelle est la distance d en m séparant Villejuif et Montlhéry ?

Conversion donnée : 1 toise=1.949 m

Distance en toises : 9 549.6 toises

Calcul de la distance en mètres (d) :

d= 9 549.6×1.949 m ≈ 18 612.6 m

Réponse :

La distance séparant Villejuif et Montlhéry est de 18 612.6 m

8-b. En utilisant les valeurs mesurées, calcule la vitesse du son dans l'air dans les conditions de l'expérience.

Données :

Distance (d) : 18 612.6 m

Temps (t) : 54.6 secondes

Formule de la vitesse (v) :

v = d/t

Calcul :

v = 18 612.6 m / 54.6 s

v≈340.9 m/s

Réponse :

La vitesse du son mesurée dans les conditions de l'expérience est d'environ 340.9 m/s.

8-c. D'après le texte, de quel paramètre dépend la vitesse du son ?

Analyse du texte : La phrase "La température de l'atmosphère était de 15.9 °C" indique que les expérimentateurs ont jugé cette donnée importante pour leurs mesures.

Réponse :

A RETENIR

D'après le texte, la vitesse du son dépend de la température de l'air.

9-a. La vitesse des ultrasons est, comme celle du son, de 1,500 m/s dans l'eau. Le signal envoyé par un dauphin met 400 ms pour revenir. À quelle distance se trouve le banc de poisson ?

1. Convertir les unités :

Vitesse (v) : 1 500 m/s

Temps de l'écho t : 400 ms. Il faut le convertir en secondes (s) :

400 ms = 0.400 s

A RETENIR

2. Déterminer le temps de trajet unique (t) :

Le temps mesuré est le temps d'aller-retour.

Le temps d'un seul trajet (dauphin → poisson) est la moitié du temps total.

t= t total /2 = 0.400 s / 2 = 0.200 s

3. Calculer la distance (d) :

d = v×t

d = 1,500 m/s×0.200 s

d = 300 m